In [2]:
%matplotlib inline
import matplotlib.pyplot as plt

Python in Astronomy

NumPy

何勃亮
中国科学院国家天文台 国家天文科学数据中心

NumPy

NumPy 是科学计算的基础，定义了在科学计算中数据是如何存储的，如何访问的。

参考

In [3]:
import numpy as np

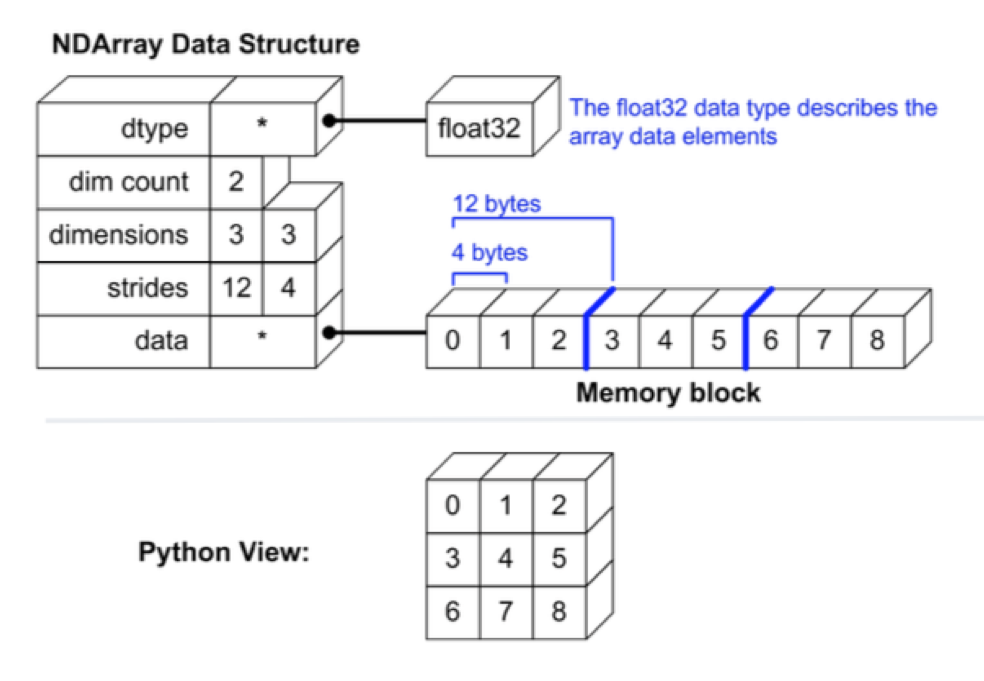
NumPy 和 SciPy

Numpy基础是数组对象ndarray

  • 数组的列类型是一致的

Numpy 数据类型

np.dtype

  • bool
  • inii
  • int8
  • int16
  • int32
  • int64
  • uint8
  • uint16
  • uint32
  • uint64
  • float16
  • float32
  • float64, float
  • complex128, complex

字符编码

  • i 整数
  • u 无符号整数
  • f 浮点
  • d 双精度浮点
  • b bool
  • D 复数
  • S 字符串
  • U unicode字符串
  • V 空
In [ ]:
np.dtype('i'), np.dtype(float)
In [ ]:
t = np.dtype('Float64')
t.char, t.type

创建 np.array 数组

In [5]:
a = np.array([1,2,3,4,5,6,7,8,9,10,11,32,12])
a.dtype
Out[5]:
dtype('int64')
In [ ]:
b = np.arange(10, dtype=np.int8)
b

Slice

一维

var[lower:upper:step]

1D

In [6]:
val = np.array([5, 12, 2, 32, 19, 71, 48])

val[1:5:2]
Out[6]:
array([12, 32])

二维

var[lower:upper:step, lower:upper:step]

2D

In [7]:
# fancy indexing

a = np.arange(1,16).reshape(3,5)
a
Out[7]:
array([[ 1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10],
       [11, 12, 13, 14, 15]])
In [8]:
a[[1,2]]
Out[8]:
array([[ 6,  7,  8,  9, 10],
       [11, 12, 13, 14, 15]])
In [9]:
a[[1,2], [3, 4]]
Out[9]:
array([ 9, 15])
In [10]:
a[a>5]
Out[10]:
array([ 6,  7,  8,  9, 10, 11, 12, 13, 14, 15])
In [11]:
# 生成函数

x = np.arange(-10,10,2)
x
Out[11]:
array([-10,  -8,  -6,  -4,  -2,   0,   2,   4,   6,   8])
In [12]:
x = np.linspace(-10, 10, 20)
x
Out[12]:
array([-10.        ,  -8.94736842,  -7.89473684,  -6.84210526,
        -5.78947368,  -4.73684211,  -3.68421053,  -2.63157895,
        -1.57894737,  -0.52631579,   0.52631579,   1.57894737,
         2.63157895,   3.68421053,   4.73684211,   5.78947368,
         6.84210526,   7.89473684,   8.94736842,  10.        ])
In [13]:
y = np.logspace(0, 10, 20, base=np.e)
y
Out[13]:
array([1.00000000e+00, 1.69268460e+00, 2.86518116e+00, 4.84984802e+00,
       8.20926306e+00, 1.38956932e+01, 2.35210258e+01, 3.98136782e+01,
       6.73920000e+01, 1.14073401e+02, 1.93090288e+02, 3.26840958e+02,
       5.53238656e+02, 9.36458553e+02, 1.58512897e+03, 2.68312340e+03,
       4.54168166e+03, 7.68763460e+03, 1.30127407e+04, 2.20264658e+04])
In [14]:
# similar to meshgrid in MATLAB
x, y = np.mgrid[0:5, 0:5]
In [15]:
x
Out[15]:
array([[0, 0, 0, 0, 0],
       [1, 1, 1, 1, 1],
       [2, 2, 2, 2, 2],
       [3, 3, 3, 3, 3],
       [4, 4, 4, 4, 4]])
In [19]:
# uniform random
np.random.rand(5)
Out[19]:
array([0.10590155, 0.7645149 , 0.31851054, 0.83186709, 0.61635669])
In [18]:
# 正态分布
np.random.randn(5,5)
Out[18]:
array([[ 1.25304372,  0.96734826, -0.11614153, -0.50205347, -0.26599271],
       [ 0.35961608,  0.40027748, -1.92450401, -0.18332112, -0.46319073],
       [ 0.07553876, -1.61579923,  0.89855496,  1.00146669, -0.66659514],
       [ 0.96992092, -0.59000221, -0.25607353,  0.15100501,  0.46731102],
       [-0.38185703, -0.19674866, -1.13602638,  0.14129038,  0.03115571]])

np.array 操作

In [21]:
a.shape = (3,4)
a

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-21-440b904f0894> in <module>
----> 1 a.shape = (3,4)
      2 a

ValueError: cannot reshape array of size 15 into shape (3,4)
In [22]:
a.reshape(5,3)
Out[22]:
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12],
       [13, 14, 15]])
In [23]:
# 展平

b = a.ravel()
In [24]:
a
Out[24]:
array([[ 1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10],
       [11, 12, 13, 14, 15]])
In [25]:
b
Out[25]:
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15])
In [26]:
b = a.flatten()
In [27]:
a
Out[27]:
array([[ 1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10],
       [11, 12, 13, 14, 15]])
In [28]:
b
Out[28]:
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15])

ravel返回的是视图，而flatten返回的是重新分配内存的新结果

In [29]:
a
Out[29]:
array([[ 1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10],
       [11, 12, 13, 14, 15]])
In [30]:
a.transpose()
Out[30]:
array([[ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14],
       [ 5, 10, 15]])
In [31]:
a
Out[31]:
array([[ 1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10],
       [11, 12, 13, 14, 15]])
In [32]:
a.T
Out[32]:
array([[ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14],
       [ 5, 10, 15]])
In [33]:
a.resize((5,3))
In [34]:
a
Out[34]:
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12],
       [13, 14, 15]])

与reshape不同，它就地更新结构

In [35]:
a.ndim
Out[35]:
2
In [36]:
a.size
Out[36]:
15
In [37]:
a.itemsize
Out[37]:
8
In [38]:
a.nbytes
Out[38]:
120
In [39]:
a.dtype
Out[39]:
dtype('int64')
In [40]:
a.T
Out[40]:
array([[ 1,  4,  7, 10, 13],
       [ 2,  5,  8, 11, 14],
       [ 3,  6,  9, 12, 15]])
In [41]:
a.tolist()
Out[41]:
[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12], [13, 14, 15]]
In [42]:
a.dot(a.T)
Out[42]:
array([[ 14,  32,  50,  68,  86],
       [ 32,  77, 122, 167, 212],
       [ 50, 122, 194, 266, 338],
       [ 68, 167, 266, 365, 464],
       [ 86, 212, 338, 464, 590]])

数组合并

concatenate((a0,a1,...,aN),axis=0)

In [43]:
x = np.array([[0, 1, 2],[10, 11, 12]])
y = np.array([[50, 51, 52],[60, 61, 62]])
In [48]:
x,y
Out[48]:
(array([[ 0,  1,  2],
        [10, 11, 12]]), array([[50, 51, 52],
        [60, 61, 62]]))
In [45]:
y
np.concatenate((x, y))
Out[45]:
array([[ 0,  1,  2],
       [10, 11, 12],
       [50, 51, 52],
       [60, 61, 62]])

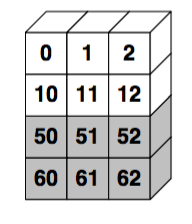
In [49]:
np.concatenate((x, y), 1)
Out[49]:
array([[ 0,  1,  2, 50, 51, 52],
       [10, 11, 12, 60, 61, 62]])

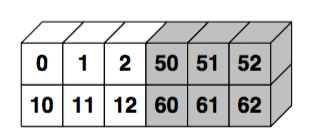
In [50]:
np.array((x,y))
Out[50]:
array([[[ 0,  1,  2],
        [10, 11, 12]],

       [[50, 51, 52],
        [60, 61, 62]]])

In [51]:
np.vstack((x,y))
Out[51]:
array([[ 0,  1,  2],
       [10, 11, 12],
       [50, 51, 52],
       [60, 61, 62]])
In [52]:
np.hstack((x,y))
Out[52]:
array([[ 0,  1,  2, 50, 51, 52],
       [10, 11, 12, 60, 61, 62]])
In [53]:
np.dstack((x,y))
Out[53]:
array([[[ 0, 50],
        [ 1, 51],
        [ 2, 52]],

       [[10, 60],
        [11, 61],
        [12, 62]]])

矩阵

在numpy中，矩阵是ndarray的子类。

矩阵函数

  • mat
  • matrix
  • bmat 复合矩阵
In [54]:
A = np.mat('1 2 3; 4 5 6; 7 8 9')
A
Out[54]:
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
In [55]:
A = np.matrix('1 2 3; 4 5 6; 7 8 9')
A
Out[55]:
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
In [56]:
A = np.mat(np.arange(1,10).reshape(3,3))
A
Out[56]:
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])

矩阵的计算

In [57]:
# 转置矩阵

A.T
Out[57]:
matrix([[1, 4, 7],
        [2, 5, 8],
        [3, 6, 9]])
In [58]:
# 逆矩阵

A.I

---------------------------------------------------------------------------
LinAlgError                               Traceback (most recent call last)
<ipython-input-58-4e066b28cdc5> in <module>
      1 # 逆矩阵
      2 
----> 3 A.I

/usr/local/lib/python3.7/site-packages/numpy/matrixlib/defmatrix.py in I(self)
    835         else:
    836             from numpy.dual import pinv as func
--> 837         return asmatrix(func(self))
    838 
    839     @property

<__array_function__ internals> in inv(*args, **kwargs)

/usr/local/lib/python3.7/site-packages/numpy/linalg/linalg.py in inv(a)
    549     signature = 'D->D' if isComplexType(t) else 'd->d'
    550     extobj = get_linalg_error_extobj(_raise_linalgerror_singular)
--> 551     ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
    552     return wrap(ainv.astype(result_t, copy=False))
    553 

/usr/local/lib/python3.7/site-packages/numpy/linalg/linalg.py in _raise_linalgerror_singular(err, flag)
     95 
     96 def _raise_linalgerror_singular(err, flag):
---> 97     raise LinAlgError("Singular matrix")
     98 
     99 def _raise_linalgerror_nonposdef(err, flag):

LinAlgError: Singular matrix
In [59]:
# Hermitian
C = np.matrix([[1j, 2j], [3j, 4j]])
C
Out[59]:
matrix([[0.+1.j, 0.+2.j],
        [0.+3.j, 0.+4.j]])
In [60]:
C.H
Out[60]:
matrix([[0.-1.j, 0.-3.j],
        [0.-2.j, 0.-4.j]])
In [61]:
# 转化成一维
A.A1
Out[61]:
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
In [62]:
np.linalg.det(A)
Out[62]:
0.0
In [63]:
# 单位矩阵

A = np.eye(3)
A
Out[63]:
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
In [64]:
B = A*10
B
Out[64]:
array([[10.,  0.,  0.],
       [ 0., 10.,  0.],
       [ 0.,  0., 10.]])
In [65]:
np.bmat("A B; B A")
Out[65]:
matrix([[ 1.,  0.,  0., 10.,  0.,  0.],
        [ 0.,  1.,  0.,  0., 10.,  0.],
        [ 0.,  0.,  1.,  0.,  0., 10.],
        [10.,  0.,  0.,  1.,  0.,  0.],
        [ 0., 10.,  0.,  0.,  1.,  0.],
        [ 0.,  0., 10.,  0.,  0.,  1.]])
In [66]:
# 零矩阵

A = np.zeros((3,3))
A
Out[66]:
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])
In [67]:
A = np.mat(np.arange(1,10).reshape(3,3))
B = np.zeros_like(A)
B
Out[67]:
matrix([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
In [68]:
# 对角阵

np.diag([1,2,3,4,5])
Out[68]:
array([[1, 0, 0, 0, 0],
       [0, 2, 0, 0, 0],
       [0, 0, 3, 0, 0],
       [0, 0, 0, 4, 0],
       [0, 0, 0, 0, 5]])
In [69]:
np.diag([1,2,3,4,5], k=1)
Out[69]:
array([[0, 1, 0, 0, 0, 0],
       [0, 0, 2, 0, 0, 0],
       [0, 0, 0, 3, 0, 0],
       [0, 0, 0, 0, 4, 0],
       [0, 0, 0, 0, 0, 5],
       [0, 0, 0, 0, 0, 0]])

矩阵计算

In [70]:
A = np.matrix('1 2 3; 4 5 6; 7 8 9')
In [71]:
A * 2
Out[71]:
matrix([[ 2,  4,  6],
        [ 8, 10, 12],
        [14, 16, 18]])
In [72]:
A + 2
Out[72]:
matrix([[ 3,  4,  5],
        [ 6,  7,  8],
        [ 9, 10, 11]])
In [73]:
A * A
Out[73]:
matrix([[ 30,  36,  42],
        [ 66,  81,  96],
        [102, 126, 150]])
In [74]:
# 求模

np.mod(A, 2)
Out[74]:
matrix([[1, 0, 1],
        [0, 1, 0],
        [1, 0, 1]])
In [75]:
A % 2
Out[75]:
matrix([[1, 0, 1],
        [0, 1, 0],
        [1, 0, 1]])

$A \times B$

$A / B $

$A^2 \times B$

In [76]:
A = np.array([1.0,6.0,2.0,5.0,8.0,9.0])
B = np.array([6.0,2.0,4.0,7.0,9.0,2.0])
A*B, A/B, A**2*B
Out[76]:
(array([ 6., 12.,  8., 35., 72., 18.]),
 array([0.16666667, 3.        , 0.5       , 0.71428571, 0.88888889,
        4.5       ]),
 array([  6.,  72.,  16., 175., 576., 162.]))

向量化函数

In [78]:
a = np.array([-3,-2,-1,0,1,2,3])

def Theta(x):
    if x >= 0:
        return 1
    else:
        return 0
In [79]:
Theta(a)

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-79-bc5d55114127> in <module>
----> 1 Theta(a)

<ipython-input-78-d5fe87216164> in Theta(x)
      2 
      3 def Theta(x):
----> 4     if x >= 0:
      5         return 1
      6     else:

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
In [80]:
Theta_V = np.vectorize(Theta)

Theta_V(a)
Out[80]:
array([0, 0, 0, 1, 1, 1, 1])

多项式

$3x^2+2x-1$

In [81]:
p = np.poly1d([3, 2, -1])
In [82]:
p(1)
Out[82]:
4
In [83]:
p.roots
Out[83]:
array([-1.        ,  0.33333333])
In [84]:
p.order
Out[84]:
2
In [85]:
x = np.linspace(0, 1, 20)
y = np.sin(x) + 0.3*np.random.rand(20)
p = np.poly1d(np.polyfit(x, y, 3))

t = np.linspace(0,1,200)

plt.plot(x, y, 'o', t, p(t), '-')
Out[85]:
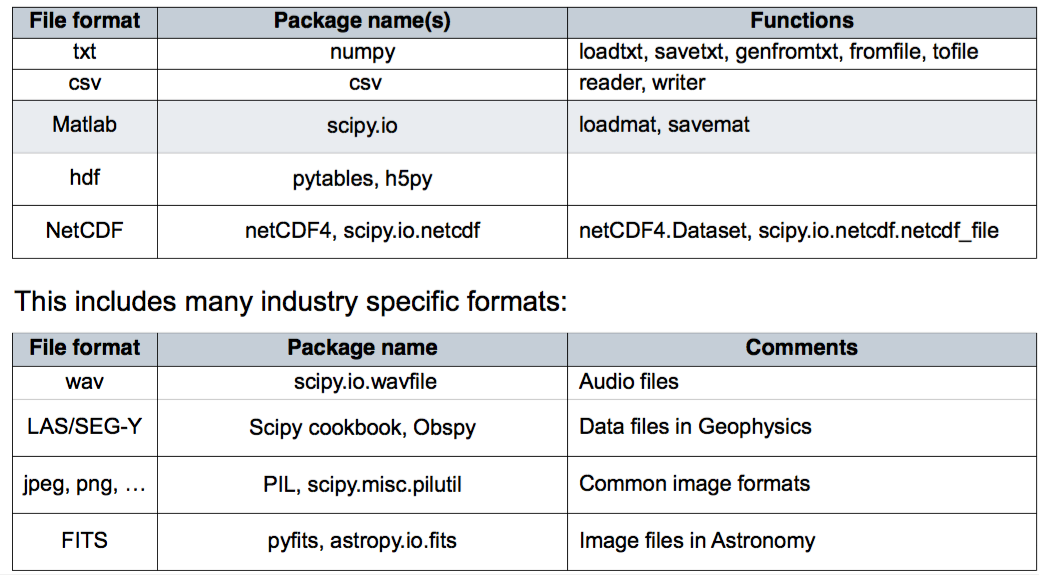
[<matplotlib.lines.Line2D at 0x1147f4bd0>,
 <matplotlib.lines.Line2D at 0x1148d3a90>]

数据文件读取

In [87]:
data = []

with open('data/mat.txt') as file:
    for line in file:
        fields = line.split()
        row_data = [float(x) for x in fields]
        
        data.append(row_data)

data = np.array(data)

data
Out[87]:
array([[1., 2., 3.],
       [4., 5., 6.]])
In [88]:
data = np.loadtxt("data/mat.txt")
data
Out[88]:
array([[1., 2., 3.],
       [4., 5., 6.]])
In [91]:
M = np.random.rand(10, 4)
np.savetxt("data/mat2.txt", M)
In [90]:
M
Out[90]:
array([[0.69368142, 0.57124763, 0.6244047 , 0.25560716],
       [0.55105268, 0.65428876, 0.58734006, 0.39434959],
       [0.01514222, 0.41617377, 0.57132712, 0.44368234],
       [0.95411287, 0.60584318, 0.47628985, 0.95512256],
       [0.54924327, 0.14040866, 0.45357402, 0.00841429],
       [0.03998804, 0.31756287, 0.29193016, 0.44689743],
       [0.78189927, 0.37743487, 0.74119805, 0.39343048],
       [0.81411988, 0.66737235, 0.61308701, 0.76448614],
       [0.64893743, 0.76569097, 0.21410647, 0.97282905],
       [0.76707317, 0.45687402, 0.04120095, 0.3617335 ]])
In [ ]:
In [92]:
np.savetxt("data/mat.csv", M, fmt="%.3f")
In [ ]:
!cat data/mat.csv
In [ ]:
dr1 = np.loadtxt('data/sample.txt')
dr1
In [ ]:
help(np.loadtxt)
In [ ]:
!head data/sample.txt
In [ ]:
dr1 = np.loadtxt('data/sample.txt',  delimiter="|", skiprows=1)
dr1
In [ ]:
!cat data/sample2.txt
In [ ]:
dtype = np.dtype([('obsid', 'S6'), ('designation', 'S19'), ('obsdate', 'S10'), ('lmjd', int)])

dr1 = np.loadtxt('data/sample2.txt',  dtype=dtype, delimiter="|", skiprows=1)

dr1
In [ ]:
dr1['lmjd']

通用函数（ufunc）

元素级的数组函数，对ndarray中的数据进行计算和操作。

  • 一元ufunc
  • 二元ufunc
  • 自定义ufunc
In [ ]:
# 一元ufunc
arr = np.arange(10)

np.cos(arr)
In [93]:
# 二元ufunc

x = np.random.randn(10)
y = np.random.randn(10)

x, y
Out[93]:
(array([-1.73611574,  0.27257883,  0.98946125, -1.28016431, -0.84533393,
         0.59951476, -1.89140112, -0.80488314,  0.20666897,  1.26553567]),
 array([-0.29983873, -0.41140903,  1.67297945, -0.35712952, -1.59784979,
         1.10375435,  0.30327272, -0.79006796, -0.78656076,  0.42386344]))
In [94]:
np.add(x, y)
Out[94]:
array([-2.03595447, -0.1388302 ,  2.66244069, -1.63729384, -2.44318372,
        1.70326911, -1.58812841, -1.5949511 , -0.57989179,  1.68939911])
In [95]:
## 自定义

def sqrt2(x,y):
    return np.sqrt(x**2 + y**2)

# input: 2, output: 1
sqrt2_uf = np.frompyfunc(sqrt2, 2, 1)

sqrt2_uf(x,y)
Out[95]:
array([1.7618175635240292, 0.49351454950041745, 1.9436804756432153,
       1.3290455852695724, 1.807681774928015, 1.2560619457035858,
       1.9155606349288492, 1.1278493940362215, 0.8132588043846879,
       1.3346313148827833], dtype=object)
In [96]:
sqrt2_uf2 = np.vectorize(sqrt2, otypes=[np.float64])
sqrt2_uf2(x,y)
Out[96]:
array([1.76181756, 0.49351455, 1.94368048, 1.32904559, 1.80768177,
       1.25606195, 1.91556063, 1.12784939, 0.8132588 , 1.33463131])

结构化数组

各列的数据类型可能不一致

In [ ]:
dtype=[('RA', np.float64), ('Dec', np.float64), ('Type', np.int16)]

sarr = np.array([(1.23293, 23.231234, 12), (12.3242, 332.47876, 34)], dtype=dtype)

sarr
In [ ]:
sarr['RA']